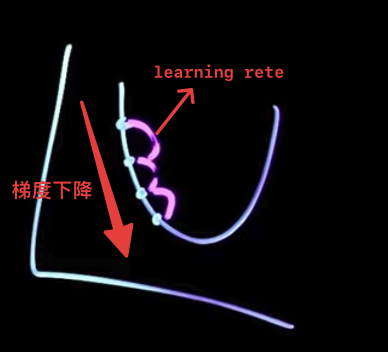
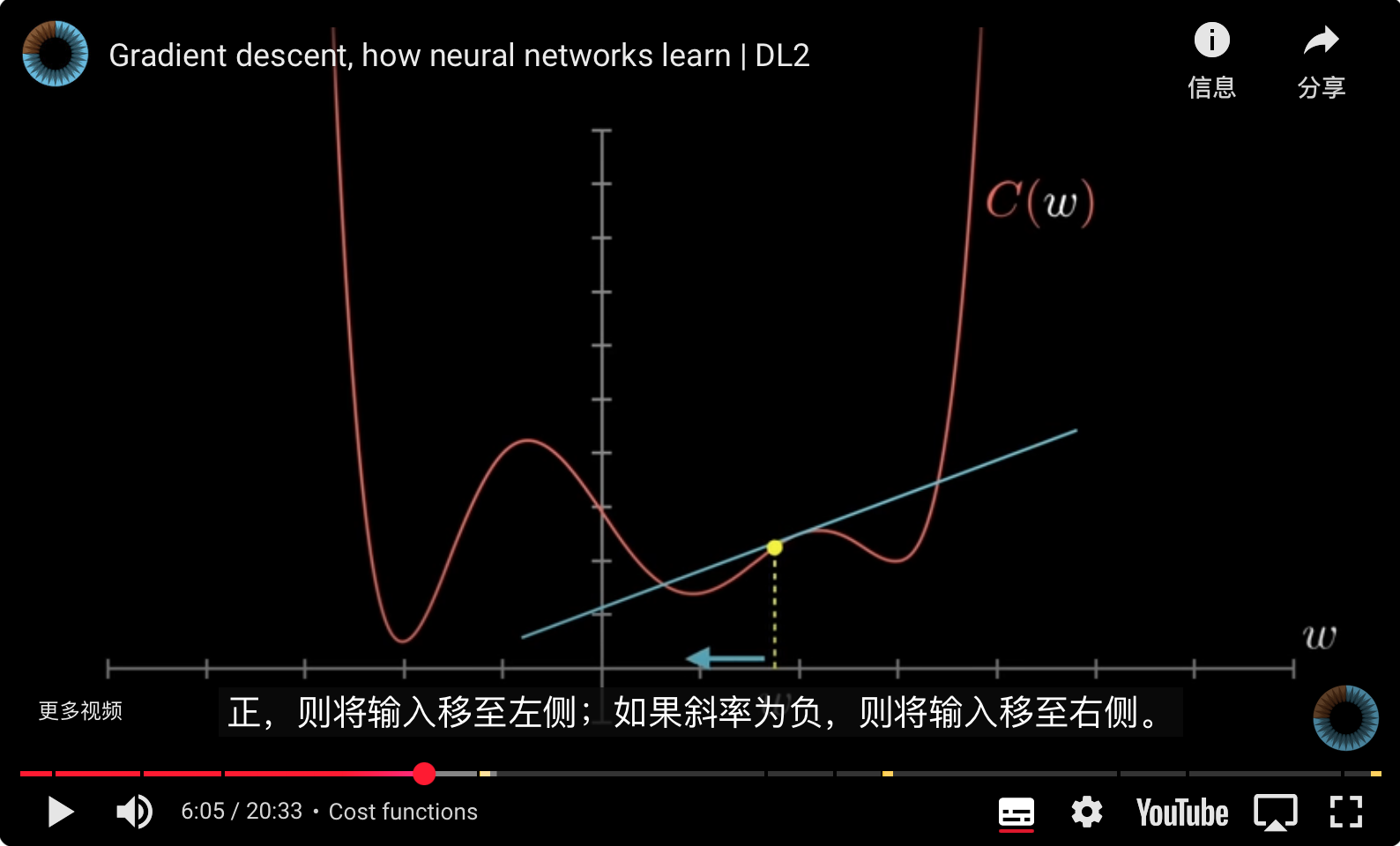
- Objective: 模型是如何学习的？当我们讨论神经网络的学习时，本质上只是在讨论最小化损失函数。 - Breadcrumb: # 概念阐释 梯度下降 gradient descent 是一种最常用的机器学习优化算法（Optimization），目的是提高模型的准确性。优化的方法是**最小化[[Loss function 损失函数]]**（cost function），以此来获得最佳预测。在调整权重和偏差时不仅仅是确定它们应该上升还是下降， 还确定这些变化的相对比例如何才能**最快**地降低成本。  *纠正：rate* ## 梯度下降法如何工作？ 梯度下降法的基本思想： - 负梯度表示**函数值下降最快的方向**，这就是梯度下降法（gradient descent）的核心逻辑：通过不断沿着负梯度的方向调整参数，使得损失函数逐步降低，趋向于最小值。 - 将成本函数看成一个山谷，你的初始参数随机放置于山谷某处。 - 你要找到**山谷最低点**（成本最小），则需要一步一步往山谷的下坡方向移动。 - **梯度（Gradient）** 是函数在当前参数处的斜率（slope）或方向。 - 沿着**负梯度方向**（下降最快的方向，相当于求负[[导数]]）移动，可以降低成本函数值。在正斜率下就向左移动，在负斜率下就向右移动，这是最快找到最小函数的方法。 -  -  # 实例 ## 假设预测房价： ### 计算[[Loss function 损失函数|成本函数]] | 房屋 | 实际价格（万元）$(y)$ | 模型预测价格（万元）$\hat{(y)}$ | 差值 | 差值平方 | | --- | ------------- | --------------------- | --- | ---- | | A | 100 | 90 | 10 | 100 | | B | 120 | 130 | -10 | 100 | | C | 80 | 95 | -15 | 225 | 此时MSE成本函数值为： $MSE=\frac{100+100+225}{3} = 141.67$ 训练过程中，模型通过调整参数，逐步降低141.67这一数值，达到更好的预测效果。 ### 用梯度下降来最小化成本函数（线性回归） - 意义： - 本质上模型只做一件事，预测下一个值$\hat{(y)}$ - 每一次成本函数的输出，都是对神经网络中的所有权重的一次微调，最终会得到一份可以部署的权重文件 - 通过迭代来降低成本函数，这是模型在训练期间唯一需要观测的数据 -  - 梯度下降的数学表示 - 以模型参数 $θ$为例（参数通常包括[[parameters 参数|参数]] $w$ 和[[偏差 bias]] $b$）： - 初始随机选择参数 $θ^{(0)}$ - 按照以下规则多轮迭代： - $\theta^{(j+1)} = \theta^{(j)} - \alpha\,\frac{\partial J(\theta^{(j)})}{\partial\theta^{(j)}}$ - 其中： - $θ^{(j)}$:第$j$次迭代的参数 - $\alpha$：**学习率（learning rate）**，决定每一步参数更新的幅度，太大会导致成本函数震荡无法收敛；太小会导致训练速度非常慢；0.01 是比较好的初始学习率，具体取值要看任务与优化器。 - $α\frac{∂J(θ^{(j)})}{∂θ^{(j)}}$:成本函数对参数的梯度 - 步骤 - **假设：** - 模型预测为 $\hat{(y)}=wx+b$ （一个输入特征 example与权重的乘积加上一个偏差） - 成本函数为 $\text{MSE}$ - **逐步降低** - 初始化随机参数 - $w=0.1 ,b=0.2$ - 计算预测值 - $\hat{(y_i)}=wx_i+b$ - 计算成本函数 - $\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2$ - $J(w,b) = \frac{1}{n}\sum_{i=1}^{n}(y_i - (wx_i+b))^2$ - 计算梯度 - 分别对$w$和$b$求偏导 - $\frac{∂J}{∂w} = -\frac{2}{n}\sum_{i=1}^{n}x_i(y_i - (wx_i+b))$ - $\frac{∂J}{∂b} = -\frac{2}{n}\sum_{i=1}^{n}(y_i - (wx_i+b))$ - 更新参数（负梯度方向，向左或向右） - $w=w-\alpha\frac{∂J}{∂w}$ - $b=b-\alpha\frac{∂J}{∂b}$ - **重复上除步骤进行迭代，直到降到最小值** |迭代次数|MSE| |---|---| |0|141.67| |1|120.3| |2|98.2| |…|…| |100|2.5| |200|0.9| # 相关内容 ## 类比 - 实际值就好像是我们想要达到的一个目标，可以是一道题的答案，可以是理想中的一篇文章，也可以是现实中解决一个问题的方法。 - 预测值就是我们每次输出、行动的结果，我们通过不断地试错来拉近输出与目标之间的距离（梯度下降）。也许一开始做得很离谱，但每次输出我们都会迭代大脑中的突触连接（更新参数），直到高质量预测、快速准确地解决问题。 - 错误集比经验集更有价值。听人说看书看别人踩过哪些坑要比看别人如何成功更有收获。我们不该怕犯错，而是应该欢迎犯错，因为发现错误就离找到正确成功一半了。 ## 梯度下降的三种类型 - **batch 批量梯度下降**：对训练集中每个点的条目求和，仅在评估完所有训练示例后才更新模型，因此称为批处理。 - 计算表现：高 - 处理时间：慢 - **stochastic gradient descent 随机梯度下降**：评估每个训练示例，但一次评估一个 - 计算表现：低 - 处理时间：快 - **mini batch 小批量梯度下降**：对训练集进行小批量处理 - 计算表现：良好 - 处理时间：良好 ## 梯度下降的局限 - 仅能解决凸问题 convex problem（U 型图），很难解决非凸问题（non-convex problem），因为很难找到全局最小值；鞍点问题（saddle），会误导梯度下降，误认为在底部。**但这一局限仅存在于一维空间，在高维度[^1]的空间中，即便陷入了鞍点[^2]，由于方向多，总会存在一个下坡的方向。** - 在更深的神经学习网络中，梯度下降可能会受到梯度消失或梯度爆炸的影响。 - 梯度消失：当梯度太小时，网络中较早的层比后面的层学习得更慢。 - 梯度爆炸：当梯度太大时，会出现梯度爆炸，这可能会产生不稳定的模型。 # 参考资料 - [gradient descent explained](https://readwise.io/reader/shared/01hzx7m4a1xvzwjbmz9zm2dayg) - [梯度下降-维基百科](https://zh.wikipedia.org/wiki/梯度下降法) - 《深度学习》谢诺夫斯基 08 - 3b1b: [[Gradient descent, how neural networks learn]] [^1]: 高维度：参数空间和特征空间： 参数空间：有多少权重（参数）就有多少维度，例如gpt3.5有1750亿个参数就有1750亿个维度。 特征空间：输入数据的特征。例如，如果输入是一个28x28像素的灰度图像，那么每个图像有784个特征（像素），特征空间就是一个784维的空间。 [^2]: 鞍点：在某些维度上会向上凸起，而在另一些维度上向下凹陷。