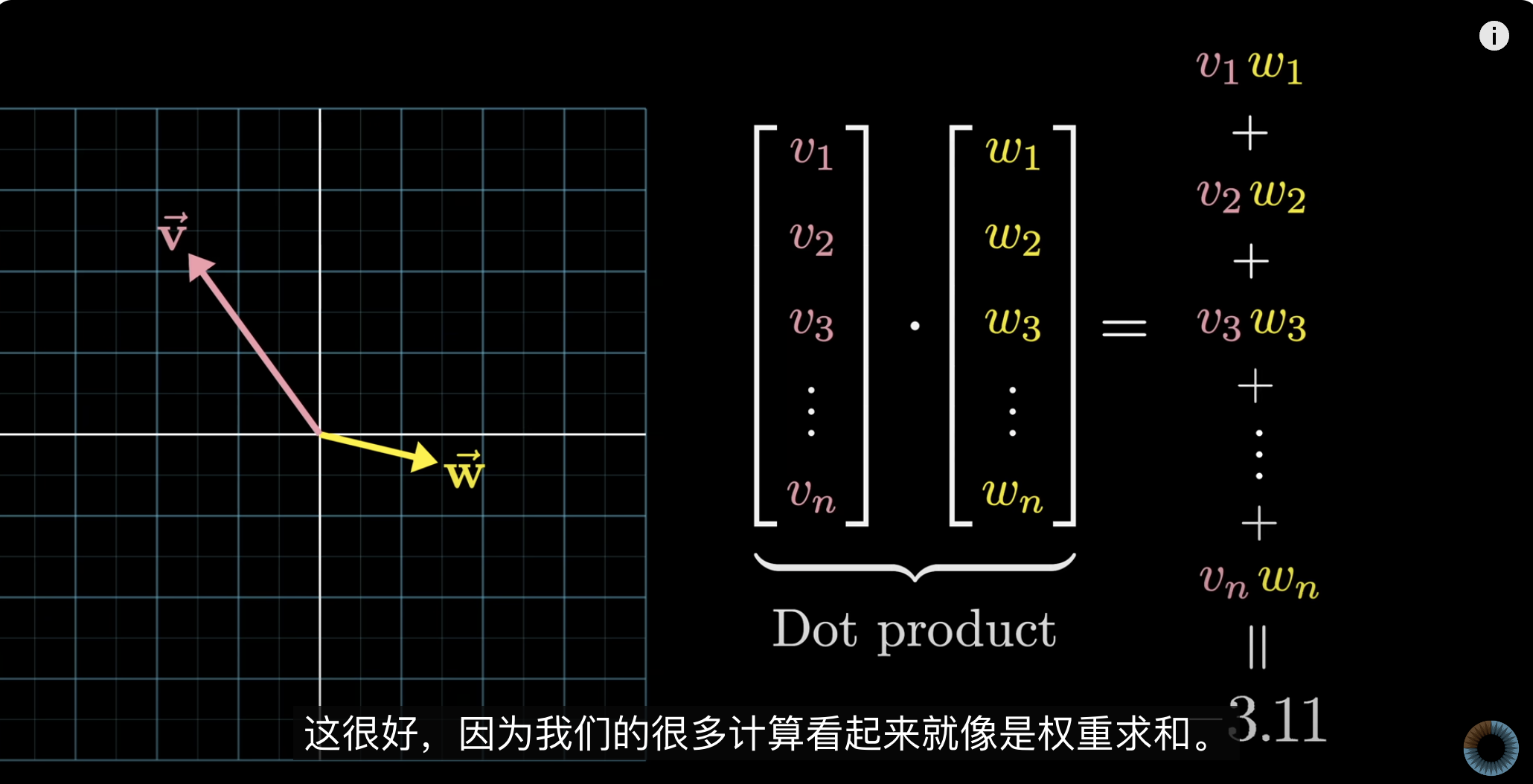
- Objective: - Breadcrumb: # 概念阐释 点积是将两个向量对应元素相乘再求和，得到一个标量，用于计算向量间的相关性。 假设我们有两个向量 $( \mathbf{a} ) 和 ( \mathbf{b} )$： $ \mathbf{a} = [a_1, a_2, \dots, a_n] \mathbf{b} = [b_1, b_2, \dots, b_n] $ 这两个向量的点积定义为： $ \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + \dots + a_n b_n = \sum_{i=1}^{n} a_i b_i $ ## 点积在 Transformer 中的作用 在 [[Transformer]] 的[[自注意力机制]]中，**点积（dot product）** 是用于计算 Query 和 Key 之间相似度的一个重要步骤。 在 Transformer 的自注意力机制中，每个输入会生成一个 **Query 向量**（查询向量）和 **Key 向量**（键向量）。点积用于计算 Query 和 Key 的相似度分数。这个相似度分数代表了 Query 向量与 Key 向量的方向一致性，也即表示**当前词和其他词在含义上的相关性。** 具体步骤如下： 1. **计算点积**：对每个 Query 和所有 Key 计算点积，得到一个相似度分数。 2. **缩放**：点积结果通常会除以 $\sqrt{d_k}$（其中 $d_k$ 是 Key 向量的维度）进行缩放，以防止数值过大。 3. **Softmax**：将这些缩放后的相似度分数通过 Softmax 转化为权重，表示当前词对其他词的「关注程度」。 通过点积操作，Transformer 能够在自注意力机制中计算出不同词之间的相似性，从而更好地捕捉输入序列中的上下文关系。 从几何角度来看，当两个向量指向==相似方向时，点积为正==；如果它们==垂直，点积为零 0==；当它们指==向相反方向时，点积为负==。  # 实例 假设将“cats”（复数）的向量表示中减去“cat”（单数）的向量表示，可能会在这个空间中找到**表示复数**概念的方向。如果将一些特定的单数名词嵌入的点积，并将其与相应的复数名词的点积进行比较。会发现这些复数名词的点积值通常比单数的更高（点积为正，相似性更高），这表明它们在某种方向上的对齐比只是单数的词更为紧密。 # 相关内容 # 参考资料 - [3B1B-Chapter 5, Deep Learning - How large language models work, a visual intro to transformers](obsidian://open?vault=Harry%E7%9A%84%E6%91%98%E5%BD%95%E7%B4%A0%E6%9D%90%E5%BA%93&file=%E7%9F%A5%E8%AF%86%E8%A7%86%E9%A2%91%2F3B1B-Chapter%205%2C%20Deep%20Learning%20-%20How%20large%20language%20models%20work%2C%20a%20visual%20intro%20to%20transformers) - [GPT-softmax/temperature/logits](https://chatgpt.com/share/672824b4-50c4-8002-91f6-b8fd4cd6e130) - 3B1B单独讲点积的视频