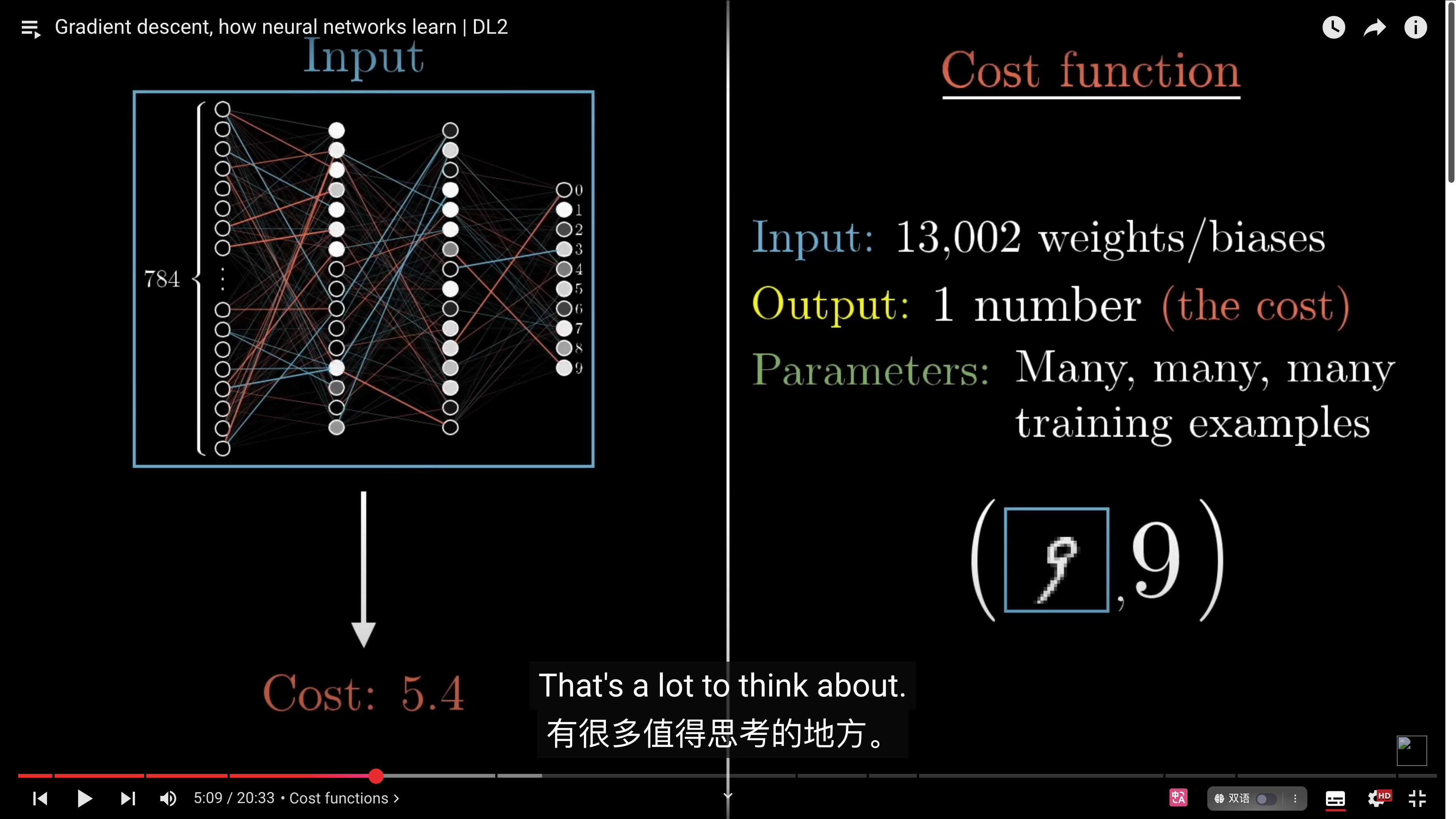
# why - 在训练机器学习模型时： - 初始时模型参数是随机设定的，导致预测值与真实值差距较大； - 通过定义成本函数，模型可量化预测的准确度； - 模型通过 **[[gradient descent 梯度下降]]** 等优化算法逐渐调整参数，最终使成本函数达到最小值，从而得到更精准的预测。 # what - 损失函数（Loss function），也叫成本函数 cost function。是机器学习中用来衡量模型预测结果与实际数据之间误差大小的一种数学函数。 - **作用**：衡量模型预测值$\hat{(y)}$与真实值$(y)$之间的差异； - **目标**：指导模型在学习过程中调整参数，使损失函数的值不断降低，直到最小化。 - **最小化损失函数**：通过基于[[gradient descent 梯度下降]]优化算法，减小模型预测和实际结果之间的差异，从而使模型更好地拟合训练数据。损失函数的目的是衡量模型的预测准确性，损失越小，表示模型的预测结果越接近真实值。 - 对于[[Hopfield Network 霍普菲尔德网络]]来说，代价函数就是能量，网络要找到能量最小化的状态； - 对于[[前馈神经网络]]来说，代价函数是输出层上的方差之和。现代分类网络更多采用交叉熵损失。 # how ## 成本函数类型 1. **均方误差（Mean Squared Error，MSE）** 1. 常用于[[回归]]任务； 2. 预测值与实际值的差距被平方，使大的误差对整体损失的影响更大。 $\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2$  ## 实际案例举例： 假设预测房价： | 房屋 | 实际价格（万元）$(y)$ | 模型预测价格（万元）$\hat{(y)}$ | 差值 | 差值平方 | | --- | ------------- | --------------------- | --- | ---- | | A | 100 | 90 | 10 | 100 | | B | 120 | 130 | -10 | 100 | | C | 80 | 95 | -15 | 225 | 此时MSE成本函数值为： $MSE=\frac{100+100+225}{3} = 141.67$ 训练过程中，模型通过调整参数，逐步降低141.67这一数值，达到更好的预测效果。 # how good # 参考资料 - [损失函数-维基百科](https://zh.wikipedia.org/wiki/损失函数) - 《深度学习》谢诺夫斯基 08 - [chatwgpt](https://chatgpt.com/g/g-p-675fc4b584188191b19370f409be9519-shen-du-xue-xi-yu-gpt-yuan-li/c/682d018f-184c-8002-941a-bf6626946442)