- Objective: - Breadcrumb: # 概念阐释 独立分量分析（Independent components analysis，ICA）是一种算法，由[[特伦斯·谢诺夫斯基]]和安东尼·贝尔发现。这种算法是[[BSS 盲源分离]]的解决办法，用来从观测信号中分离出信号源。通过ICA，我们可以得到一组独立成分（声音源、图像特征），这些成分可以看作是对原始数据的基本特征表示。 ## 基本概念： - **观测信号**：例如麦克风记录的声音信号可以有多个声音源：说话者、背景音乐、盘子碟子碰撞的声音； - **源信号**：独立的原始信号，从观测中分离出的成分，独立性假设在统计学中意味着一个信号的值不会影响其他信号。 - **非高斯信号源**：ICA假设源信号是非高斯分布的。非高斯性是指信号的分布不同于正态分布（也叫做高斯分布，钟形曲线）。这种特性是分离信号的重要依据，因为混合信号的分布会趋向于高斯。 - **混合模型**：ICA 假设观测信号是多个源信号通过未知的**线性混合**过程生成的。非线性观测信号可能需要更加复杂的算法来处理。 - **[[unsupervised learning 无监督学习]]算法**：与[[perceptron 感知器]]的[[Supervised learning 监督学习]]算法不同，ICA 是一种无监督学习算法。 # 实例 ## 语音信号分离 假设我们有两个麦克风在一个房间内录制了两个人的对话。混合信号如下： ```scss x1(t) = a11 * s1(t) + a12 * s2(t) x2(t) = a21 * s1(t) + a22 * s2(t) ``` 其中 $x1(t)$和 $x2(t)$ 是麦克风录制的混合信号， $s1(t)$ 和$s2(t)$ 是两个独立的说话者信号， $a11,a12,a21,a22$ 是混合系数。 通过ICA，我们希望从 $x1(t)$ 和 $x2(t)$ 中恢复出 $s1(t)$ 和 $s2(t)$。 现在我们使用的每一款**降噪耳机**和手机中都有独立成分分析算法。 ## 图像信号分离 > 独立分量分析的**独立成分**是局部化的定向边缘滤波器，类似于猫和猴子的视觉皮层中的简单细胞（[[眼睛]]）。 局部化的定向边缘滤波器： - **局部化**：它们只对图像的某个局部区域敏感。 - **定向**：它们对某个特定方向的边缘（例如水平、垂直或斜向的边缘）敏感。 换句话说，ICA就像是装了一个过滤器（[[Filter 滤波器]]，通过它可以过滤掉图像中大量冗余的信息（例如天空的像素），只提取出有用的独立源信号。这些独立源信号就是图片中对我们有意义的**边缘和纹理**信息。  # 相关内容 ## 数学 > ICA是一个线性变换。这个变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。 - **线性变换**：ICA是一种liner 线性变换，这意味着它使用 **[[线性代数]]** 的方法将输入数据转换为输出数据。具体来说，它通过**矩阵运算**将观测信号转换成独立信号。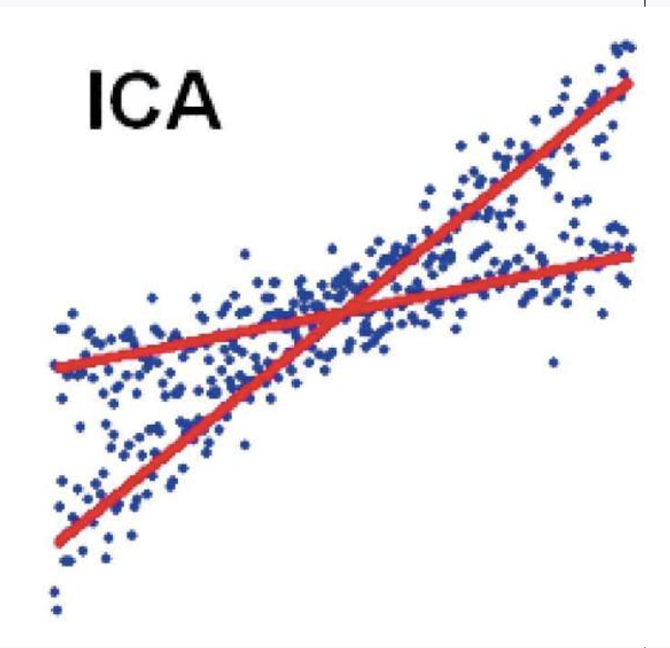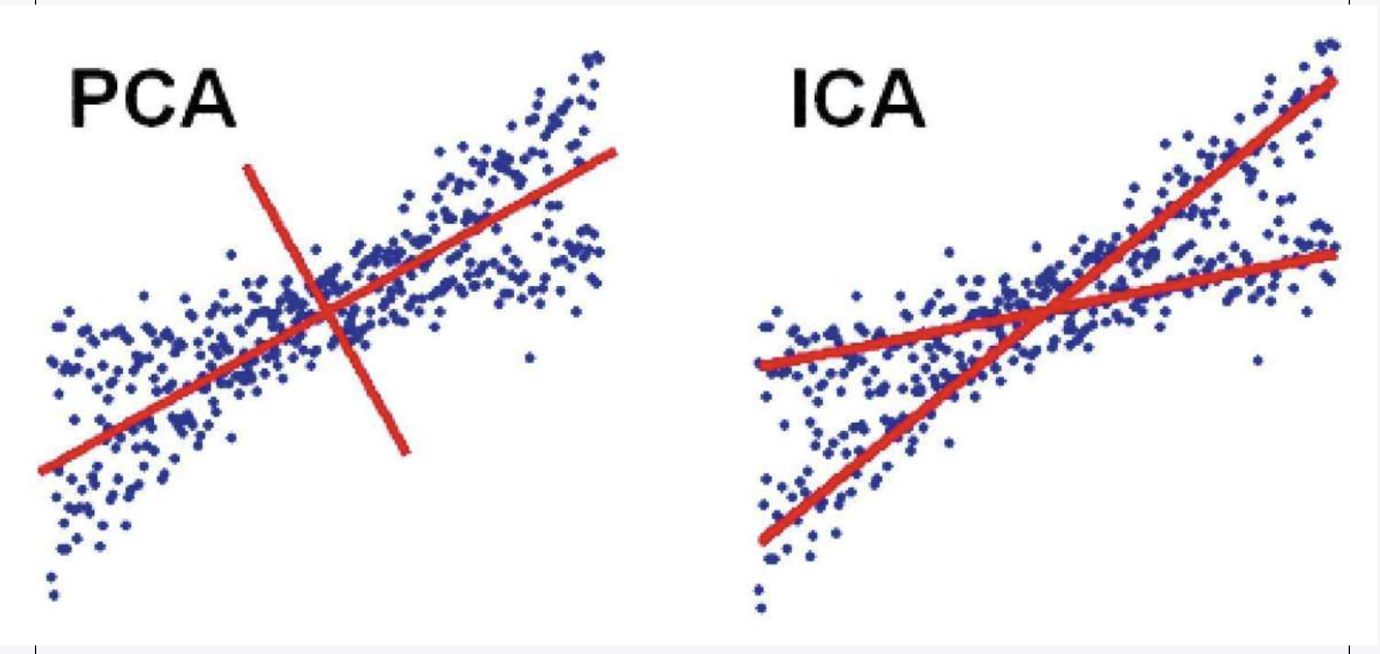  ## ICA 与 PCA 的对比 - [[PCA 主成分分析]]：无监督学习技术，它挑选出两个信号等分的方向，将它们的混合程度最大化，并且PCA轴始终相互垂直。 - ICA找到沿点的方向伸展的轴，来表示分离的信号，这些轴可能不是垂直的。  ## 无监督学习 与[[perceptron 感知器]]不同，ICA 是一种无监督学习，对输出单元的目标是什么并不知道，目的是使声源彼此独立，即使不独立也会去掉相关性。无监督学习可以发现新的模式和结构。 # 参考资料 - [独立成分分析-维基百科](https://zh.wikipedia.org/wiki/独立成分分析) - [线性代数-维基百科](https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E4%BB%A3%E6%95%B0)