# videos checklist
- [x] seen?
- [x] note-taking? thinking about it?
- [ ] share?
# why
# what
- ### Summary
- 本视频介绍了神经网络的基本概念和结构,强调了人脑如何轻松识别数字,而机器学习则面临挑战。通过可视化的方式,讲解了神经元的工作机制,以及如何构建和训练一个简单的神经网络来识别手写数字。视频还提到神经网络的多层结构及其激活值的计算方法,并为后续学习提供了基础。
- ### Highlights
- 🧠 **人脑的识别能力**:人脑能够轻松识别不同形式的数字,即使它们的像素值差异很大,这引发了对机器学习的思考。
- 🖥️ **神经网络结构**:神经网络由输入层、隐含层和输出层组成,输入层对应图像的每个像素,输出层表示识别的数字。
- 🔢 **激活值的计算**:每个神经元的激活值通过加权和计算得出,并通过sigmoid函数转换为0到1之间的值,决定神经元是否被激活。
- 🔄 **权重与偏置**:神经网络的学习过程涉及调整权重和偏置,以优化识别结果,理解这些参数的意义有助于改善网络表现。
- 📊 **矩阵运算的重要性**:神经网络的运作依赖于矩阵乘法,简化了计算过程,使得实现和优化变得更高效。
- ### keyword
#神经网络 #深度学习 #机器学习
# how
- Timeline: [0:00](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1)
- Introduction example [1:07](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=67s)
- Series preview [2:42](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=162s)
- What are neurons? [3:35](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=215s)
- [[ANN 人工神经网络]]中的[[人工神经元 neuron]]
- [[激活值 activation]]
- Introducing layers [5:31](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=331s) 
- input layer
- 28x28 神经元的输入图像
- 
- hidden layers
- why 2 layers? 随机展示
- output layer
- 输出为 0-9 个神经元,[[ANN 人工神经网络]]的运行方式是一层激活值决定下一层激活值。**how?**
- 
- Why layers? [8:38](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=518s)
- 当我们在识别数字时,会把数字变成一些组件,比如 9 是由`○和|`组成的,8 是由`○和○`组成的。理想情况下,我们希望隐藏层的最后一层是这样的组件,但是这对于计算机来说很难。
- 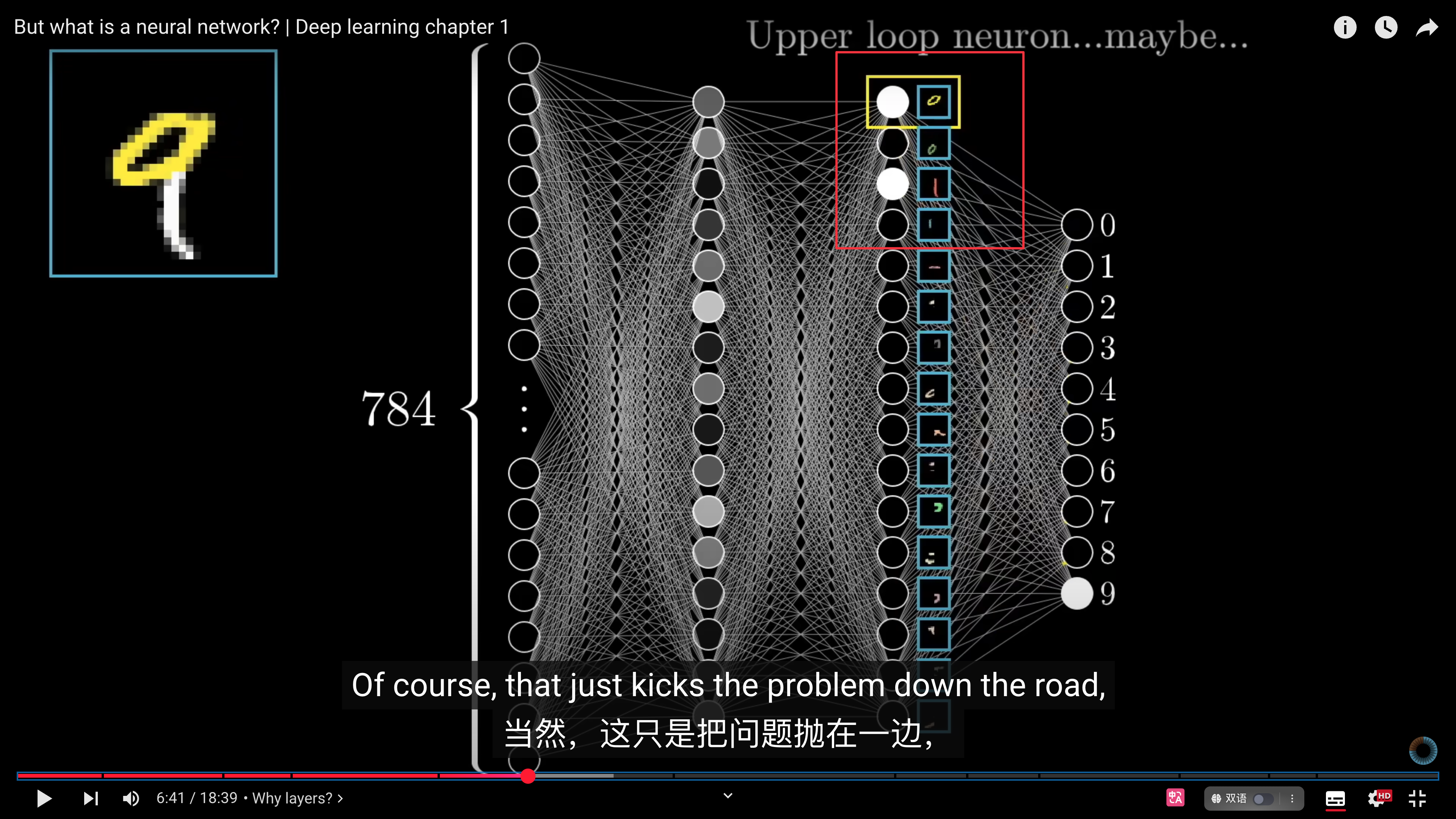
- 更好的方法是将组件继续向下分解成小的边缘edges。但是**神经网络真的会这样工作吗?** [[CNN 卷积神经网络]]
- 
- Edge detection example [11:34](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=694s)
- 一层神经元的激活值是如何决定下一层的激活值的?这些联结是做什么的?
- 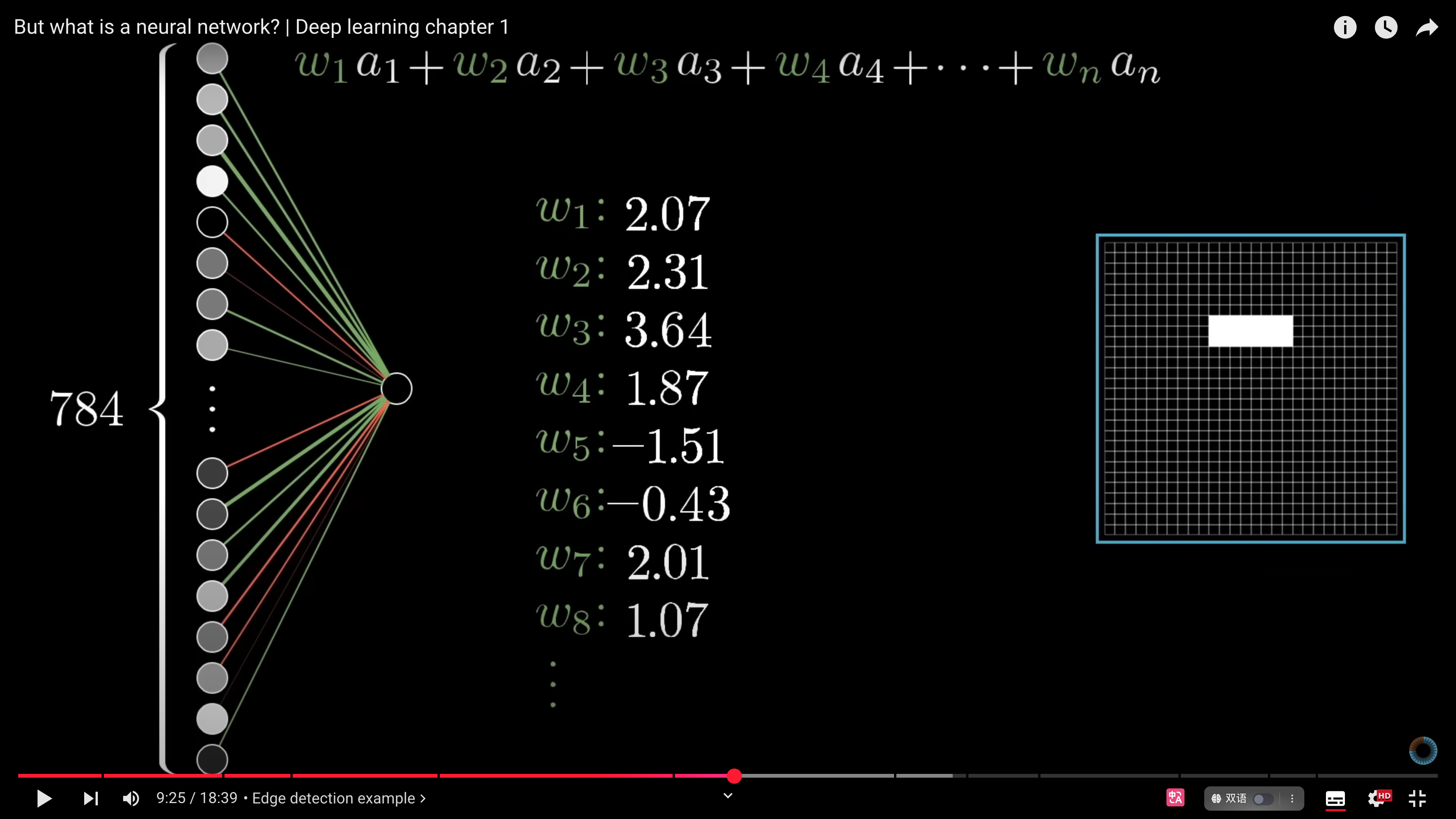
- 这些联结 parameter 赋予一些随机参数[[parameters 参数|weights]],第二层的[[人工神经元 neuron]]的激活值等于: $σ(w_1a_1+w_2a_2+w_3a_3+...+w_na_n) $
- $f$为[[Sigmoid]]函数,可以让[[激活值 activation]]保持在 0~1之间
- 一个神经元的结果相当于一块小的边缘
- Counting weights and biases [12:30](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=750s)
- [[偏差 bias]] #todo
- $neuron(function) = σ(w_1a_1+w_2a_2+w_3a_3+...+w_na_n+b_0) $
- How learning relates [13:26](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=806s)
- [[machine learning 机器学习|机器学习]],从计算的角度讲就是计算机找到一个正确的权重和偏差的过程
- 
- Notation and linear algebra [15:17](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=917s)
- 激活值的更加紧凑简洁的写法是用[[矩阵向量乘法]]
$ neural network(function) = σ(\begin{bmatrix}
w_0,_0 w_0,_1...w_0,_n \\
w_1,_0 w_1,_1...w_1,_n \\
.\\
.\\
.\\
w_k,_0 w_k,_1...w_k,_n
\end{bmatrix} * \begin{bmatrix}
a_0(^0)\\
a_1(^0)\\
.\\
.\\
.\\
a_n(^0)\\
\end{bmatrix} + \begin{bmatrix}
b_0\\
b_1\\
.\\
.\\
.\\
b_n
\end{bmatrix}= \begin{bmatrix}
?\\
?\\
.\\
.\\
.\\
?\\
\end{bmatrix})$
- 机器学习的很大一部分与[[线性代数 linear algebra]]有关,如果想深入了解,看[线性代数的本质](https://youtu.be/kYB8IZa5AuE?si=9QmPrLVgQOW9PFb0)这个视频。 #todo
- Recap [16:27](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=987s)
- things that holds a number其实不准确,更准确的说,神经元是一个函数,整个神经网络是一个大函数。
- Some final words [17:03](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi&index=1&t=1023s)
- ReLU vs Sigmoid
- [[Sigmoid]]现在来看已经过时了,训练[[Deep Learning 深度学习|深度神经网络DNN]]更好的方法是[[ReLU]]激活函数。 #todo
# how good
# inbox
# todo
# ref.
- [ ] link
# related.
# archive.