- Objective: 提高模型准确性、优化模型 - Breadcrumb: # 概念阐释 - 反向传播算法（Backpropagation）是一种使多层人工神经网络（深度学习）成为可能的算法。从网络输出层的损失函数（成本函数）开始，逐层计算梯度，每一层的梯度都取决于下一层的误差。这种依次回传的计算过程被称为“链式法则”，形成一环扣一环的传播路径，最终回溯到输入层。 - 反向传播算法（Backpropagation）最早由 Paul Werbos 于 1974 年提出基础思想，并于 1986 年由 Geoffrey Hinton、大卫·鲁姆哈特和罗纳德·威廉姆斯在《自然》（Nature）杂志上系统阐述，使其成为深度学习的基石。这篇论文至今被引用超过 4 万次。 - **数学角度**：通过反向传播衡量成本函数 $C_0$​ 对各个权重$w$、偏置$b$的“敏感度”，即梯度（[[偏导数]]）。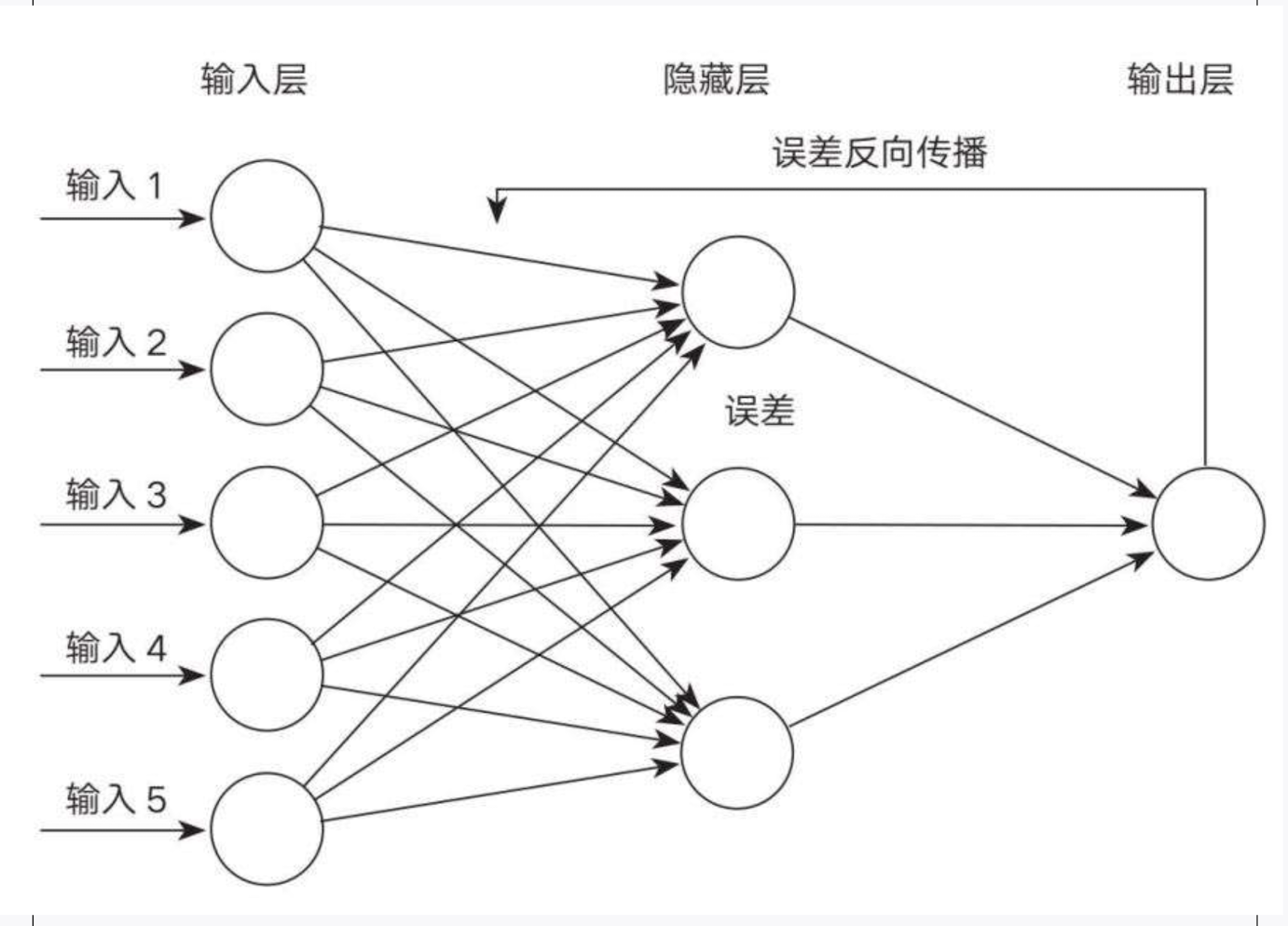  ## 解决了什么问题 反向传播算法解决了多层神经网络的训练难题，提供了高效更新参数的路径。换句话说，在拥有很多参数（权重和偏置）的神经网络中，如果我们不知道如何根据输出**误差**来调整每一层的参数，网络就没法自动学会完成任务。 下面我用几个要点来说明它究竟解决了什么难题： 1. **多层网络的梯度计算问题** - 在没有反向传播之前，人们无法有效地计算多层网络各个参数需要如何更新。 - 当网络层数增加时，如果想逐个用手推导或用别的方式计算误差对每个参数的影响，会变得极其复杂。 - **反向传播**则提供了一种系统、可重复的算法，**通过从输出层（预测结果）开始，把误差一层一层地“反传”回去，进而计算每一层的梯度，更新参数。** 2. **减少计算复杂度** - 反向传播使用了[[链式法则]]（微积分中的一个重要工具）来高效地求偏导数，避免做冗余的重复运算。 - 要更新数以亿计的参数，就必须高效、精确地拿到每个参数对损失的影响；链式法则提供了唯一可行的数学途径。如果没有反向传播，就得在每一次更新时，对每个参数独立做计算，既费时又容易出错。 3. **让深度学习成为可能** - 正是因为有了反向传播，深度神经网络才变得可训练，才带来了近年来人工智能的高速发展。 - 不管是卷积神经网络（CNN）、循环神经网络（RNN），还是更复杂的Transformer，几乎都需要依赖反向传播来更新数以百万计、甚至上亿计的参数。 4. **统一了各种类型的网络训练** - 反向传播并不限于全连接网络，也可应用在卷积网络、循环网络、图网络等各种结构中。它等于给深度学习提供了一个“通用学习公式”，只要能写出损失函数（目标），就能用反向传播去求解各参数的梯度，进行训练。 # 实例 ## 比喻 反向传播明确了哪些动作能拉近与目标的距离，哪些动作会远离目标，我们通过增加有益动作，减少不利动作，逐步逼近目标。 ## 自动驾驶 1989 年，一名叫 Dean Pomerleau的一年级博士生，用反向传播算法重建了汽车自动驾驶软件 ALVINN。通过观察人类如何在道路上行驶来学习自动驾驶。 ## 文字识别 1989 年，[[Yann LeCun 杨立昆]]利用反向传播算法和美国邮政部门提供的大量手写笔迹数据创建了 LeNet 系统。20 世纪 90 年代中期，美国超过 10%的支票读取系统是由 LeNet 完成的。 ## 话语网络 特伦斯·谢诺夫斯基（Terrence J. Sejnowski）和查尔斯·罗森伯格（Charles Rosenberg）在1980年代末和1990年代初研究了话语网络（Narrative Networks NETtalk），可以大声朗读的神经网络。该神经网络模型要解决的问题是输出英语的正确发音。模型通过由 2 万个字母的布朗语料库的训练后，泛化效果非常好，并且模型自主发现了英语发音的规律，证明了反向传播算法能够有效地表征英语的音韵。 通过对模型进行[[Cluster analysis 聚类分析]]，发现模型之所以能够获得正确发音是因为正确识别了元音和辅音，这和人类的学习方法一样。 话语网络的另一应用是，通过一串氨基酸序列来预测蛋白质的二级结构。这一应用的结果要好于生物物理学的最佳方法，机器学习在分子序列中的首次应用并开启了一个新的领域-生物信息学 bioinformatics. # 相关内容 ## 计算过程 - **[[前向传播 Forward Propagation]]** - 输入数据通过神经网络各层传播，直至输出层，计算得到网络的预测输出。 - **计算损失函数：** - $C_0 = (a^{(L)} - y)^2$ - 实际值：$a^{(L)}$ - 期望值：$y$ - 其中，最后一层的激活值$a^{(L)}$由前一层的激活值、权重和偏置决定，然后再经过一个非线性函数（如sigmoid 或 ReLU）计算出来： - $a^{(L)}=σ(w^{(L)}a^{(L-1)}+b^{(L)})$ - 简化括号内的内容为：$a^{(L)}=σ(z^{(L)})$ - **计算梯度：** - 我们从损失函数向前追溯，通过每一层计算误差的梯度，再用[[gradient descent 梯度下降]]的方法来减小损失函数的误差，使得模型在下一次预测时会更接近目标 token。 - **更新权重（Weight Update）：** - 使用[[gradient descent 梯度下降]]或其变种（如随机梯度下降法、Adam优化算法等）更新每个神经元的权重。其中，$w_{ij}$​是权重，$\eta$是学习率，$\frac{\partial E}{\partial w_{ij}}$是[[Loss function 损失函数]]对权重的偏导数。 $ w_{ij} = w_{ij} - \eta \frac{\partial E}{\partial w_{ij}} $ # 参考资料 - [反向传播 - GPT](https://chatgpt.com/share/29d94d96-8d51-4f1e-8005-494aaedd7252) - [一文弄懂神经网络中的反向传播法](https://www.cnblogs.com/charlotte77/p/5629865.html) - [反向传播算法-维基百科](https://zh.wikipedia.org/wiki/反向传播算法) - 《深度学习》谢诺夫斯基 08 - [卷积神经网络与反向传播算法的区别](https://readwise.io/reader/shared/01jmbctq2qcjfa6015gqyd11wr)