# what ## 基本逻辑门： - 逻辑与 AND，线性可分 - 逻辑与非 NAND，线性可分 - 逻辑或 OR，线性可分 - 异或 XOR，排除或，线性不可分 ### 1. **AND 运算** **AND** 运算的规则：只有两个输入都是“红色”（即 **1**）时，输出才是“红色”（即 **1**）；其他情况输出是“蓝色”（即 **0**）。 |输入1|输入2|输出|解释| |---|---|---|---| |蓝色 (0)|蓝色 (0)|蓝色 (0)|0 AND 0 = 0| |蓝色 (0)|红色 (1)|蓝色 (0)|0 AND 1 = 0| |红色 (1)|蓝色 (0)|蓝色 (0)|1 AND 0 = 0| |红色 (1)|红色 (1)|红色 (1)|1 AND 1 = 1| ### 2. **NAND 运算** **NAND** 运算是 **AND** 运算的反面，两个输入都是“红色”（即 **1**）时，输出是“蓝色”（即 **1**）；其他情况输出是“红色”（即 **0**）。 |输入1|输入2|输出|解释| |---|---|---|---| |蓝色 (0)|蓝色 (0)|红色 (1)|0 NAND 0 = 1| |蓝色 (0)|红色 (1)|红色 (1)|0 NAND 1 = 1| |红色 (1)|蓝色 (0)|红色 (1)|1 NAND 0 = 1| |红色 (1)|红色 (1)|蓝色 (0)|1 NAND 1 = 0| ### 3. **OR 运算** **OR** 运算的规则：只要其中有一个输入是“红色”（即 **1**），输出就是“红色”（即 **1**）；否则，输出是“蓝色”（即 **0**）。 |输入1|输入2|输出|解释| |---|---|---|---| |蓝色 (0)|蓝色 (0)|蓝色 (0)|0 OR 0 = 0| |蓝色 (0)|红色 (1)|红色 (1)|0 OR 1 = 1| |红色 (1)|蓝色 (0)|红色 (1)|1 OR 0 = 1| |红色 (1)|红色 (1)|红色 (1)|1 OR 1 = 1| ### 4. **XOR 运算** **XOR** 运算的规则：只有当两个输入不同（一个是红色，一个是蓝色）时，输出是“红色”（即 **1**）；当两个输入相同（两个都是红色或两个都是蓝色）时，输出是“蓝色”（即 **0**）。 |输入1|输入2|输出|解释| |---|---|---|---| |蓝色 (0)|蓝色 (0)|蓝色 (0)|0 XOR 0 = 0| |蓝色 (0)|红色 (1)|红色 (1)|0 XOR 1 = 1| |红色 (1)|蓝色 (0)|红色 (1)|1 XOR 0 = 1| |红色 (1)|红色 (1)|蓝色 (0)|1 XOR 1 = 0| ### 总结 - **AND**：只有两个输入都是 **1** 时，输出才是 **1**，其他情况输出 **0**。 - **NAND**：除了两个输入都是 **1** 时输出 **0**，其他情况下输出 **1**。 - **OR**：只要有一个输入是 **1**，输出就是 **1**，否则输出 **0**。 - **XOR**：当两个输入不相同时，输出 **1**，当两个输入相同时，输出 **0**。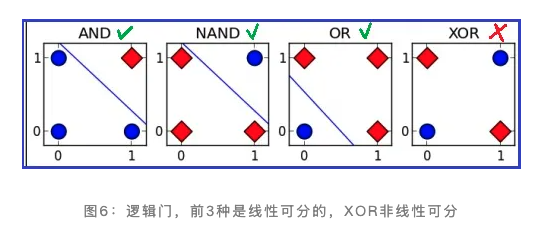  前 3 种属于线性可分问题，可以被[[perceptron 感知器]]解决，但 XOR 为线性不可分，这是感知器被“遗弃”的原因。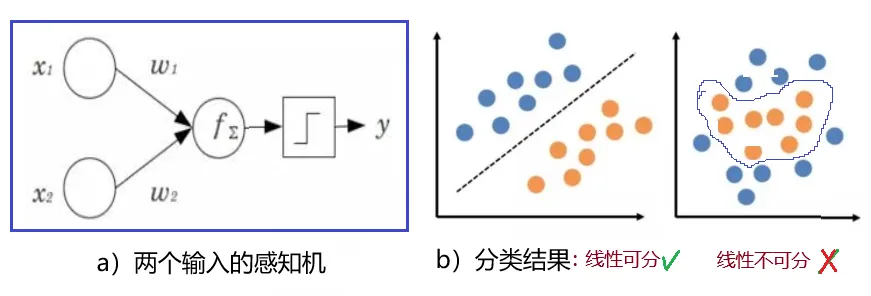 # why ## 为什么[[perceptron 感知器]]不能解决异或问题？ - 因为感知器无法模拟 **“非线性不可分”** 问题，例如异或门问题。 - **只有1个输出**：感知器的架构是多个输入和一个输出。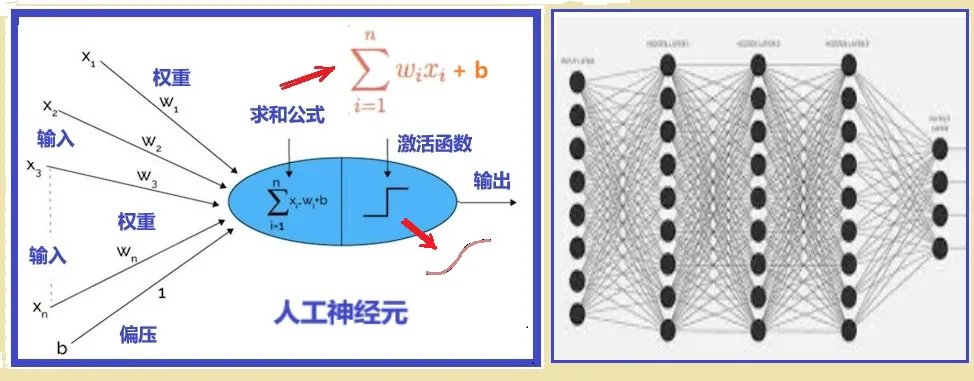 -  - **只能分成两类**：求和公式 $z=\sum_{i=1}^n w_i x_i + b$ 是 n 维空间中的一个超平面，分类就是指讲这个超平面分为两个部分； - **只有一个输出**：感知器使用[[activation function 激活函数]]中的阶梯函数进行分类，输出 0 或 1； - 所以感知器只能处理输入为线性可分的问题，如果是线性不可分的，则无法处理，即异或问题。 -  # how ## [[MLP 多层感知器]]如何解决异或问题 - 非线性可分问题在多层神经网络中得到了解决，因为多层感知器中多了一个隐藏层 - 隐藏层和输出层神经元都是拥有激活函数的功能神经元。激活函数进行分类，如果增加一个带非线性激活函数的隐藏层相当于增加了一个空间维度，就可以将非线性不可分问题变成非线性可分了； - 如图：决策计算生成两条直线，就可以区别异或问题了。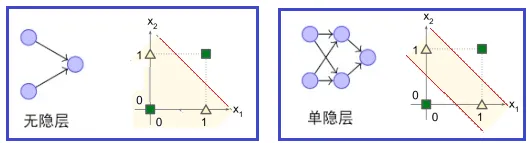  # how good # Ref. - [AI 江湖：神经网络兴衰史](https://readwise.io/reader/shared/01jbp11cqt4thg1tnt0eb3ab59)