# 为什么重要?
反向传播算法(Backpropagation)最早由 Paul Werbos 于 1974 年提出基础思想,并于 1986 年由 Geoffrey Hinton、大卫·鲁姆哈特和罗纳德·威廉姆斯在《自然》(Nature)杂志上系统阐述,使其成为深度学习的基石。这篇论文至今被引用超过 4 万次。
反向传播算法之所以重要,是因为它解决了多层神经网络的训练难题,让深度学习成为可能。该算法从网络输出层的损失函数(成本函数)开始,逐层计算梯度,每一层的梯度都取决于下一层的误差。这种依次回传的计算过程被称为“[[链式法则]]”,形成一环扣一环的传播路径,最终回溯到输入层。
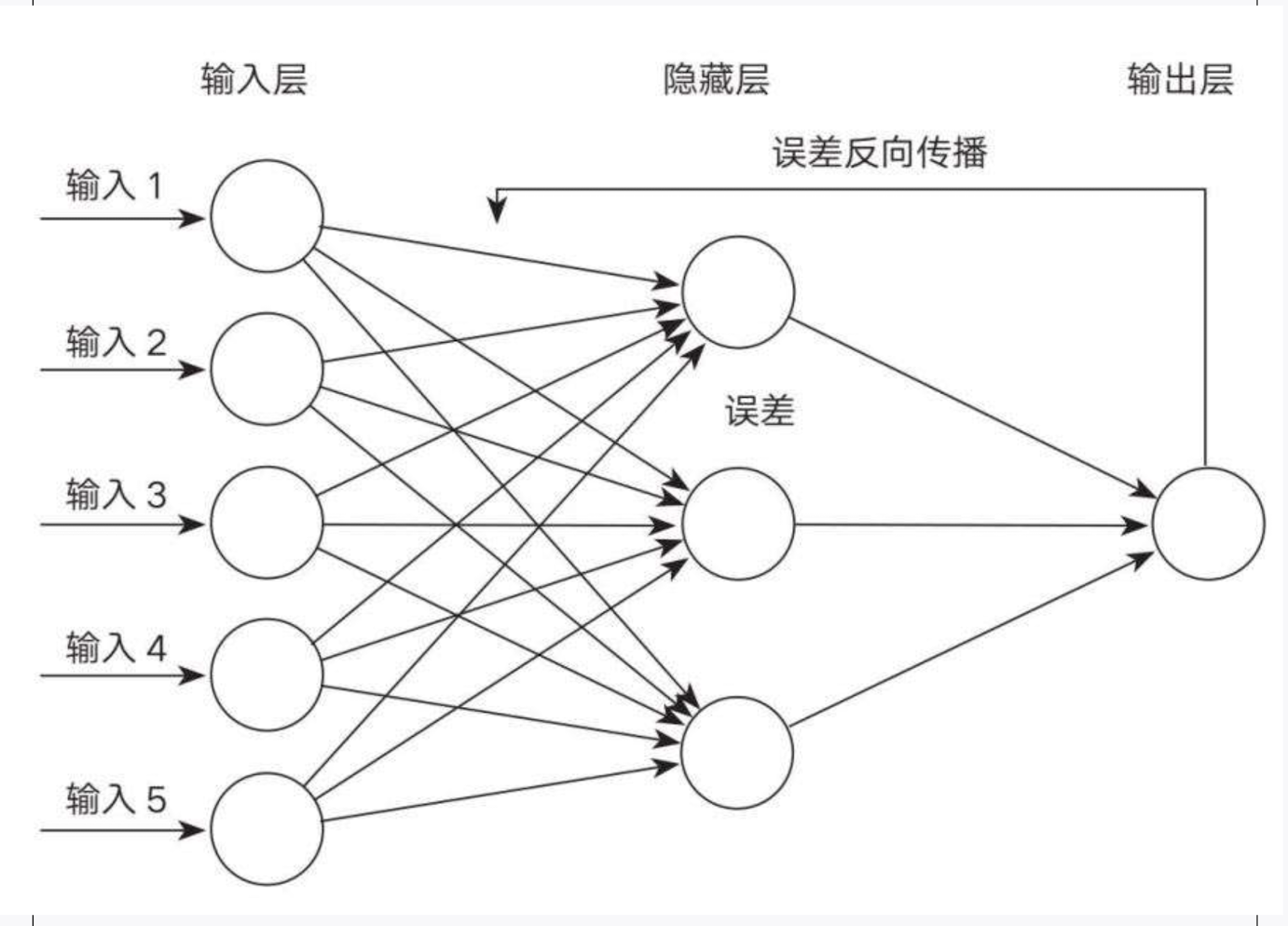
# 算法原理
神经网络通过不断更新权重和偏置,逐渐缩小预测值与实际值之间的误差,使模型的预测越来越准确。
如何确定权重更新的方向和幅度?关键在于计算**成本函数对每个权重的敏感程度,也就是梯度(偏导数)**,它既衡量“方向”也衡量“幅度”。这类似于在山谷中下山的比喻,梯度告诉我们如何以最快的方式朝着山谷的最低点迈进。
换句话说,反向传播明确了哪些动作能拉近与目标的距离,哪些动作会远离目标,我们通过增加有益动作,减少不利动作,逐步逼近目标。
# 实例说明
假设目标是让神经网络准确识别数字“2”。未经训练时,网络激活值随机,我们期望得到数字“2”的激活值为 `1`,其他数字的激活值为 `0`。
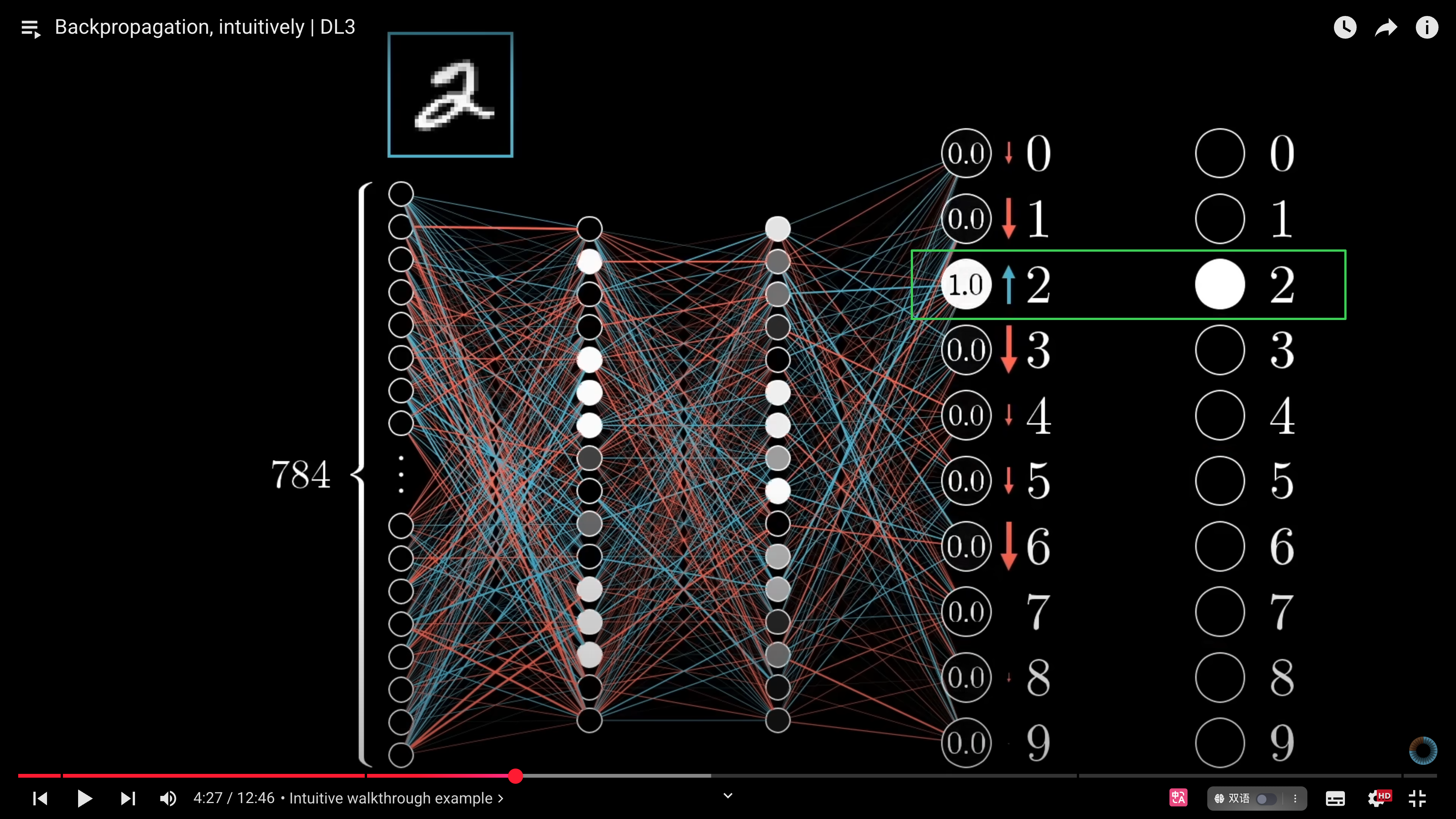
### zoom in
放大来看,数字“2”节点的激活值受权重与偏置的影响。尽管**无法直接更改激活值,但我们能调整权重(w)和偏置(b)以间接控制激活值**。具体而言,连接上一层较大激活值的权重影响更明显,连接较小激活值的权重则影响较小。因为权重与激活值的乘积关系。
$0.2 = σ(w_0a_0+w_1a_1+w_2a_2+w_3a_3+...+w_{n-1}a_{n-1}+b_0)$

除了增加权重和偏置外,我们还可以通过改变上一层的激活值$a$的方式来影响数字 2 的激活值。不过也是通过调整对应的权重与偏置实现。
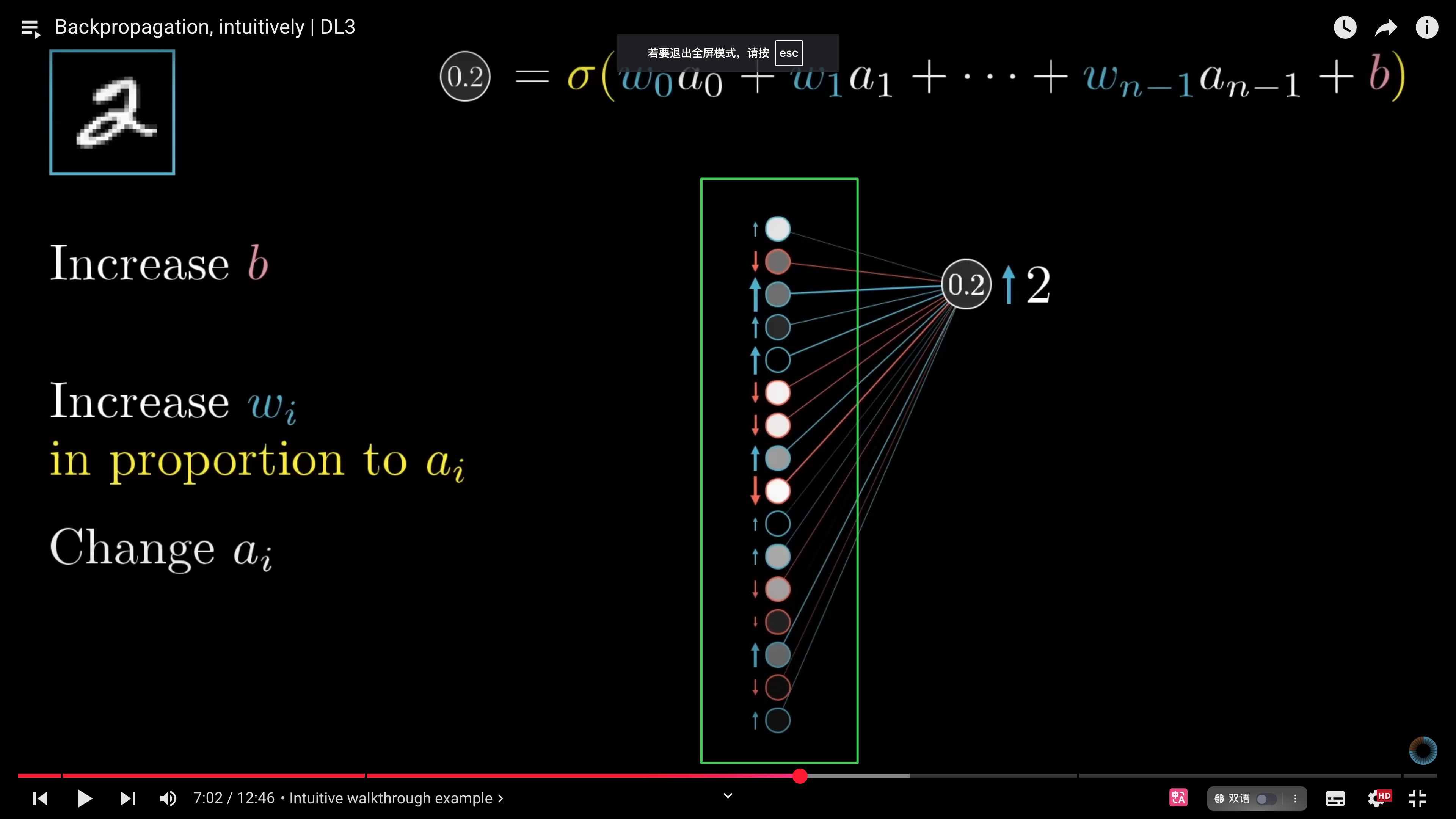
### zoom out
整体视角下,现在我们回到整个神经网络。为了能够识别数字 2,我们不仅要调整与“2”连接的权重和偏置来影响前一层的激活值,同时其他数字的权重和偏置也会对这一层激活值有影响。当把所有的影响都加在一起,就会得到一个总权重变化和总偏置变化的数值。**将所有影响合并后逐层回传,这便是反向传播算法的本质。**

以上的过程,我们只把识别数字 2 作为目标来改变权重和偏置,但如果只是这样的话,这个神经网络将会把所有数字都识别成数字 2。所以在实际训练中,不只针对数字“2”,而是对所有数字类别进行梯度计算并求取平均,进而更新权重。
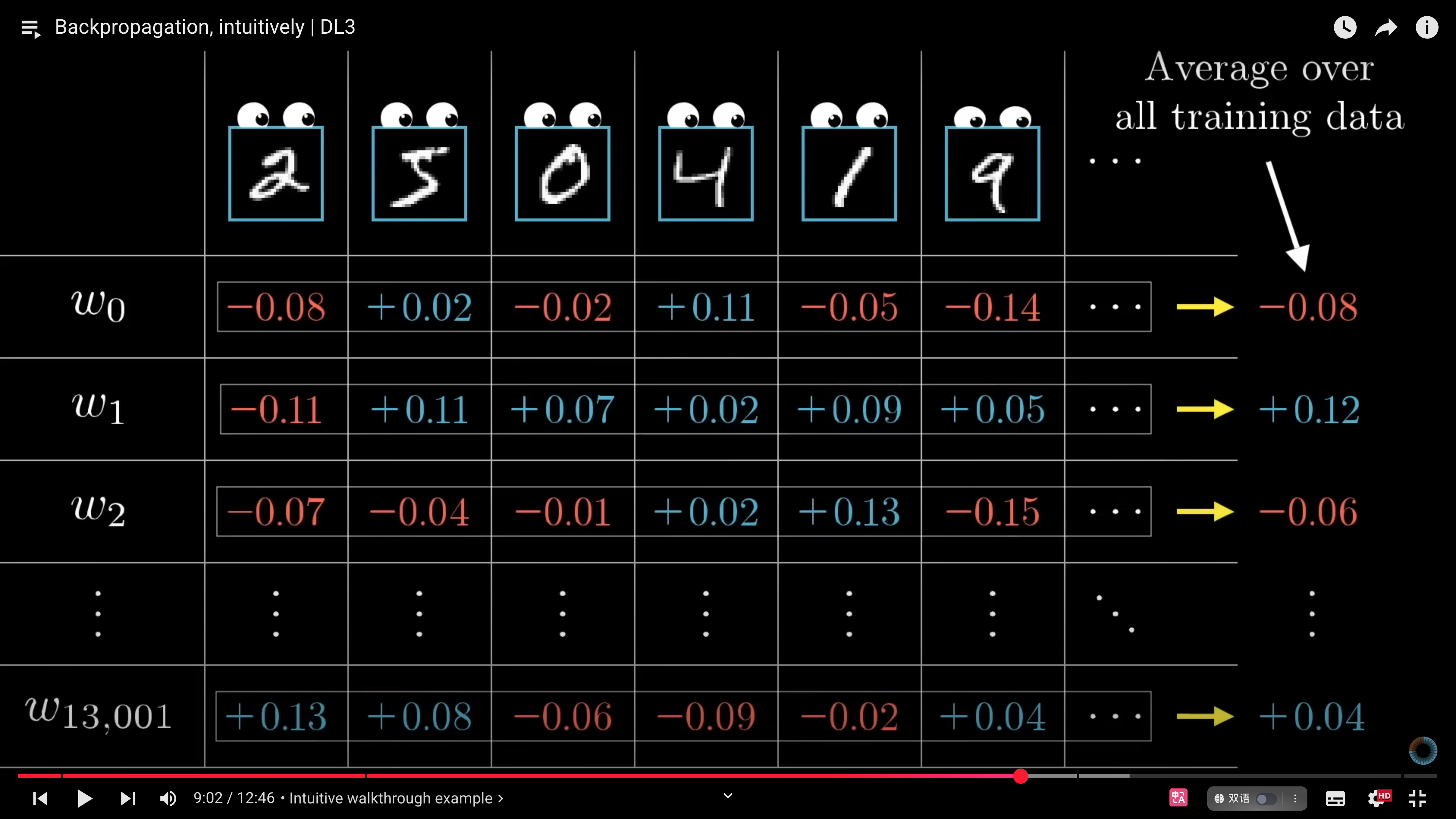
损失函数在参数空间里的梯度向量:
$∇C(w_1,w_2,...w_{13,001})=\begin{bmatrix}
-0.08\\
+0.12\\
-0.06 \\
.\\
.\\
.\\
+0.04
\end{bmatrix}$
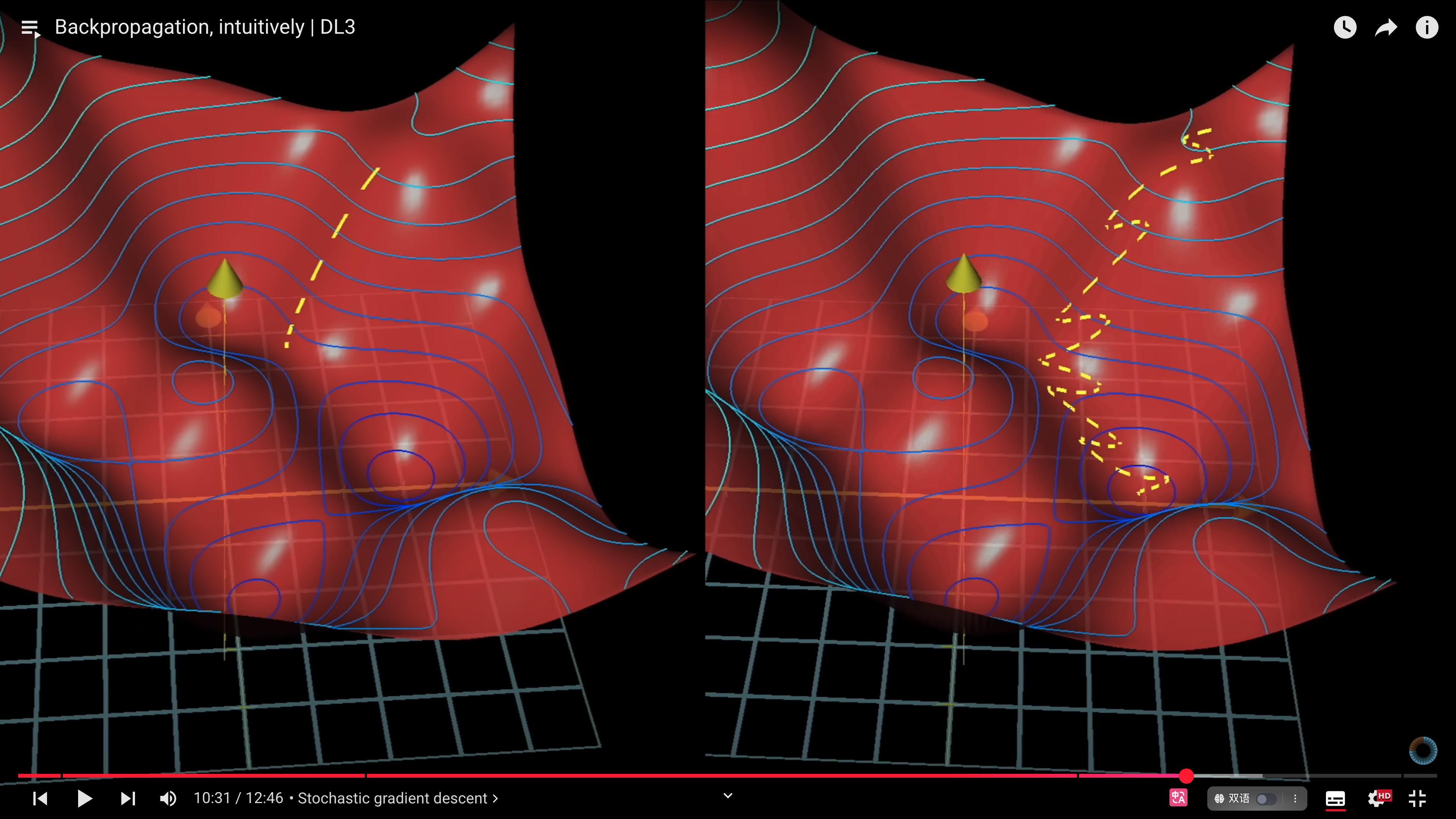
# 随机梯度下降
计算机需要花很长的时间来计算完整数据集的梯度,计算每个梯度时都要使用所有的样本数据。因此,实际训练时常用随机梯度下降(Stochastic Gradient Descent,SGD)。SGD 的思想可追溯到 Robbins-Monro 1951 年的随机近似方法。SGD 将训练数据分成小批次,逐批次计算梯度,虽然不是完整梯度,却是高效的近似解。
如果用一个比喻,SGD 类似醉汉下山,虽然路径弯曲不确定,却比谨慎前进更快速接近目标。这也与现实中的行动策略类似,追求完美可能寸步难行,更有效的方式是快速行动并迭代优化。
# 数学推导
对于深度学习的数学,我的理解非常有限,以下内容仅为个人理解。未来,我会阅读《深度学习的数学》这本书,并将学习笔记分享出来。
机器学习本质上就是在做数学运算,反向传播的数学基础是微积分的链式法则。这里以单神经元网络示例简化说明。
### 目的
计算成本函数$C_0$对权重$w^{(L)}$的敏感程度(梯度)。如图中那些红/蓝箭头“↑/↓”。

| 符号 | 直白说法 | 技术含义 |
| ------------- | ------------- | ------------------------------------------------------ |
| **红色↓箭头** | “这里得往下调!” | 该权重/偏置对应的梯度为 **负数**。如果它再变大,损失 $C$ 反而会上升,所以必须把它 **减小**。 |
| **蓝色↑箭头** | “这里需要加码!” | 该权重/偏置的梯度为 **正数**。只要把它 **增大**,损失 $C$ 就会下降。 |
| **箭头长度/粗细** | “用力大小” | 在完整版动画里,箭头越长/越粗,代表梯度绝对值越大——也就是那一项对损失最“敏感”,更新幅度应更大。 |
| **成排的 “+” 号** | “这里本来是一张权重矩阵” | 黑板上密密麻麻的连接权重,作者只用 + 号占位,方便在其上叠加箭头显示方向。 |
### 推导步骤
我们还是把问题进行简化,假设一个神经网络,每层只有一个神经元。最后一个神经元的激活函数为$a^{(L)}$,上一层的激活函数为$a^{(L-1)}$。
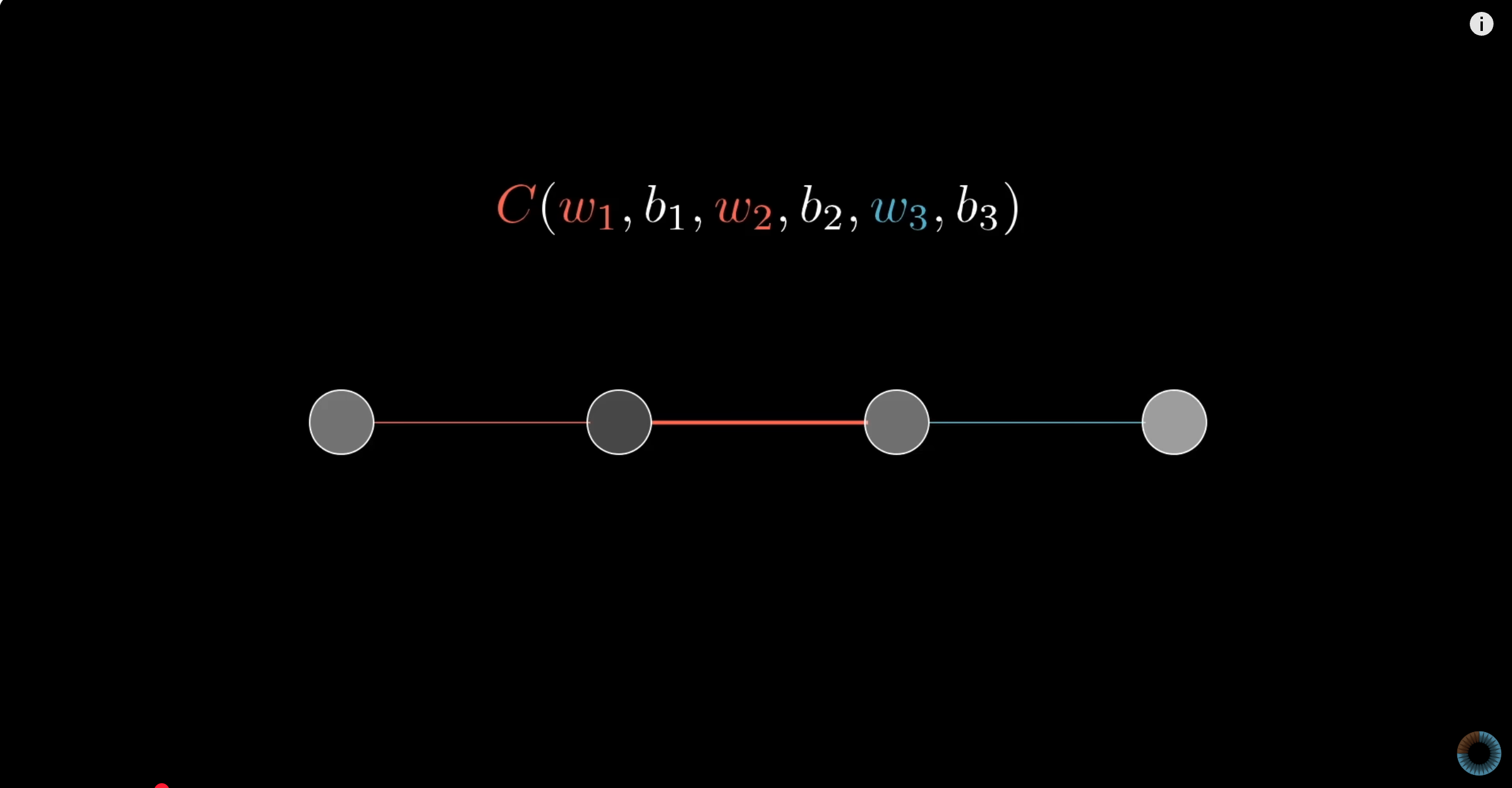
#### 计算损失函数:
假设损失函数为均方误差(MSE):
$C_0 = (a^{(L)} - y)^2$
- 实际值为$y$
- 激活值为:$a^{(L)}=σ(w^{(L)}a^{(L-1)}+b^{(L)})$
- 其中$(w^{(L)}a^{(L-1)}+b^{(L)})$合并为$z^{(L)}$:$a^{(L)}=σ(z^{(L)})$
#### 计算梯度:
链式法则将求导过程拆分成三个小步骤,先计算每一步的导数,再相乘:
$\frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{(L)}}{\partial w^{(L)}} \times \frac{\partial a^{(L)}}{\partial z^{(L)}} \times \frac{\partial C_0}{\partial a^{(L)}}$
$\frac{\partial z^{(L)}}{\partial w^{(L)}} = a^{(L-1)}$, $\frac{\partial a^{(L)}}{\partial z^{(L)}} = σ'(z^{(L)})$, $\frac{\partial C_0}{\partial a^{(L)}}= 2(a^{(L)} - y)$
#### 更新权重:
得到梯度后,权重更新规则为:
$w_{new} \leftarrow w_{old} - \eta \frac{\partial C_0}{\partial w^{(L)}}$
其中,$\eta$ 为学习率,控制更新步长。
# Ref.
- 《深度学习》p133-134
- [[Backpropagation, intuitively, calculus]]