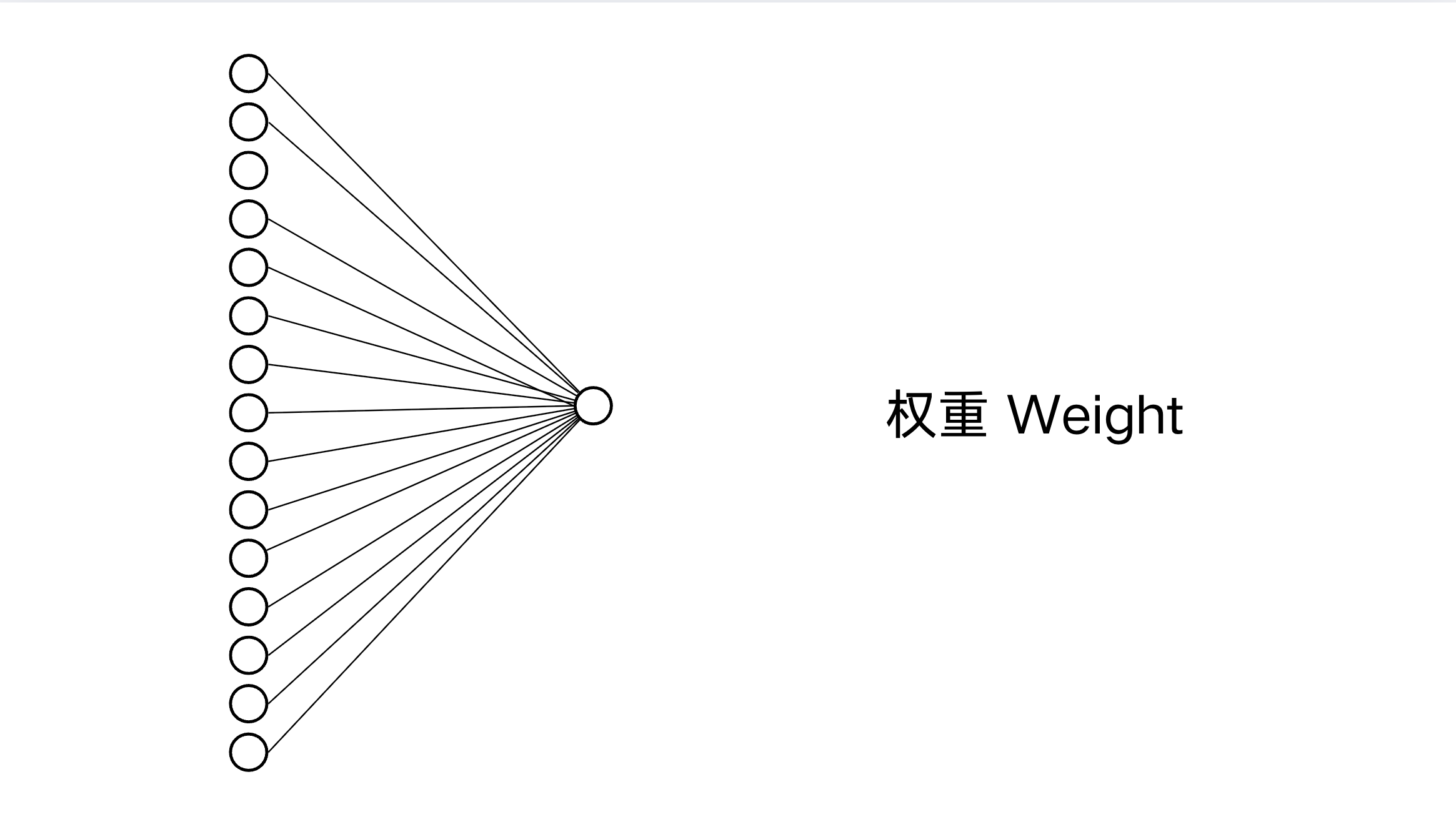
以下内容是3b1b频道视频《But what is a neural network》的学习笔记。 ## 点：神经元  神经网络的最小基本单位是神经元。每个神经元存储着一个数字，这个数字称为“激活值”，用以表示神经元的活跃程度。过去常用的激活函数如sigmoid，会将激活值压缩到0到1之间，但现代网络最常用的是ReLU（线性整流函数），它允许激活值范围从0到正无穷，完全不受上限限制。这篇文章主要介绍的是 sigmoid 函数的神经网络。 人工神经元和我们大脑中神经元的开关类似：激活的神经元对应于某个概念或特征，比如当我们看到苹果🍎时，一组特定的神经元就会同时活跃起来。 ## 线：权重  神经元之间的联结被称为权重（weight），类似我们大脑中突触的连接。实际上，人类大脑每个皮层神经元大约拥有7000个突触。神经网络通过这些联结决定下一层的激活值，其计算方法如下： $σ(w_1a_1+w_2a_2+w_3a_3+...+w_na_n+b_0)$ - $w$: 权重，这些联结一开始是一些参数，但是随着机器的学习，这些参数会不断优化，直到得到一组正确的权重。 - $a$: 神经元中的激活值，由上一层的输出提供。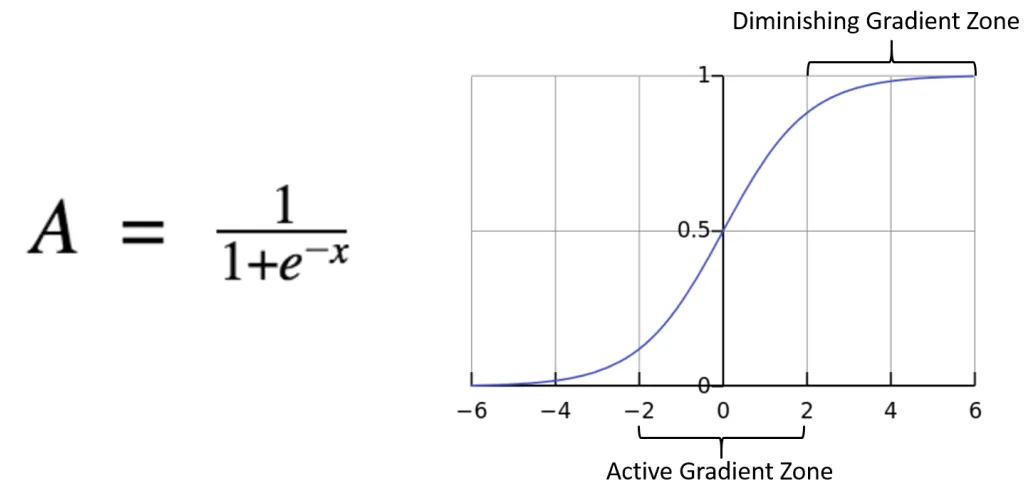 - σ：sigmoid，也被称为 s 型函数或逻辑函数，它能够让后面的权重和保持在 0~1之间，因为如前面所说，激活值是一个 0-1 之间的数字。但是现代更常用ReLU。 -  - $b_0$: 决定神经元激活的敏感性和阈值。它不仅决定神经元激活的难易程度，还能在训练过程中更快地收敛。例如，如果我们希望神经元在加权总和大于10时才激活，可以将偏差$b$设为-10。这样，小于10的值即便经过权重相乘，也不会触发激活。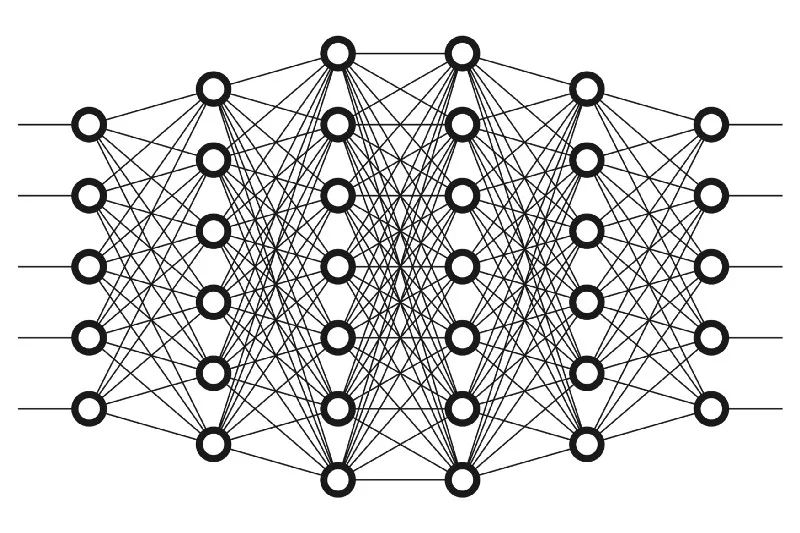 ## 面：神经网络  神经网络由大量神经元和权重组成，可简单分为输入层、隐藏层和输出层。这个结构受人脑启发，模拟人类神经元之间相互连接的工作方式。 输入数据经过网络，权重不断调整，最终形成能够精准识别模式的网络，就像大脑通过学习不断强化或弱化突触连接一样。 刚刚我们知道了一个神经元激活值的函数，但是对于神经网络来说更加简洁的写法是： $ neural network（function） = σ(\begin{bmatrix} w_0,_0 w_0,_1...w_0,_n \\ w_1,_0 w_1,_1...w_1,_n \\ .\\ .\\ .\\ w_k,_0 w_k,_1...w_k,_n \end{bmatrix} * \begin{bmatrix} a_0(^0)\\ a_1(^0)\\ .\\ .\\ .\\ a_n(^0)\\ \end{bmatrix} + \begin{bmatrix} b_0\\ b_1\\ .\\ .\\ .\\ b_n \end{bmatrix}= \begin{bmatrix} ?\\ ?\\ .\\ .\\ .\\ ?\\ \end{bmatrix})$ ## 神经网络如何识别图像？ 以经典的手写数字识别（[[MNIST 数据集]]）为例：一个 28×28 像素的图片（共 784 个像素），比如写着数字“9”，我们一看就懂，但机器如何学会识别呢？ 首先，这 784 个像素对应网络的输入层，共 784 个神经元。输出层为 10 个神经元，分别对应数字 0 到 9。最终目标是机器准确地点亮代表数字“9”的那个输出神经元。 如果我们用的是简单的多层神经网络（全连接网络），机器其实是在隐藏层内自动学习哪些组合模式更可能是数字 9。但现代更加有效的做法，是使用[[CNN 卷积神经网络]]。CNN 会专门处理图像数据，通过卷积核自动地找出边缘、线条和图案，逐层组合为更复杂的图案： 1. 第一层（卷积层）找出数字“9”的边缘特征； 2. 第二层组合这些特征为更明确的结构（比如圆弧、竖线）； 3. 再下一层把结构组合成完整数字“9”。 这个过程也是受到人类视觉识别的启发，运用了类似人类的视觉系统识别图像的步骤。